\ 無料で体験できます /

中学受験における算数の「割合」の重要性について、今回はお話していきたいと思います。
4年生前半までの算数の学習では、実生活の中にあるものの値段や個数など、子どもたちがイメージしやすいものの数量を求めていくのがほとんどです。
しかし、「割合」の概念が入ってくることで急に苦手意識を持つお子さんも少なくありません。
ここでは、中学受験における「割合」の位置づけを確認しながら、克服していくポイントを整理していきます。
「割合」は数学の原点
割合は、数学の基本的な概念の一つで、分数や小数、比と深く関わっています。
割合とは、ある量が別の量に対してどれくらいの大きさかを示すもので、「全体の中でどのくらいの割合か」を理解することで、日常生活にも役立つ考え方です。
例えば「100人のうち30人がAさんのファンなら、Aさんのファンは全体の30%」と表現でき、これが割合の考え方です。
小学生のうちに、分数や小数の四則計算(足し算、引き算、掛け算、割り算)をしっかり身につけると、割合をより自由に使いこなせるようになります。
こうした基礎的な理解は、将来的に中学・高校で学ぶより高度な数学、さらには様々な場面で役立つ土台となってきます。
これは割合を計算する際にも必要になるので、段階を踏みながら丁寧に理解を深めていくことが大切です。
小学4年生で分数や小数の概念を学ぶと、「分数→小数」や「小数→分数」への変換を覚える場面も出てきます。
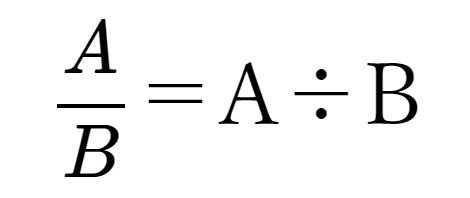
このように分数を小数に変換できますが、よくでてくる分数と小数の変換はまとめて暗記しておくのが効果的です。
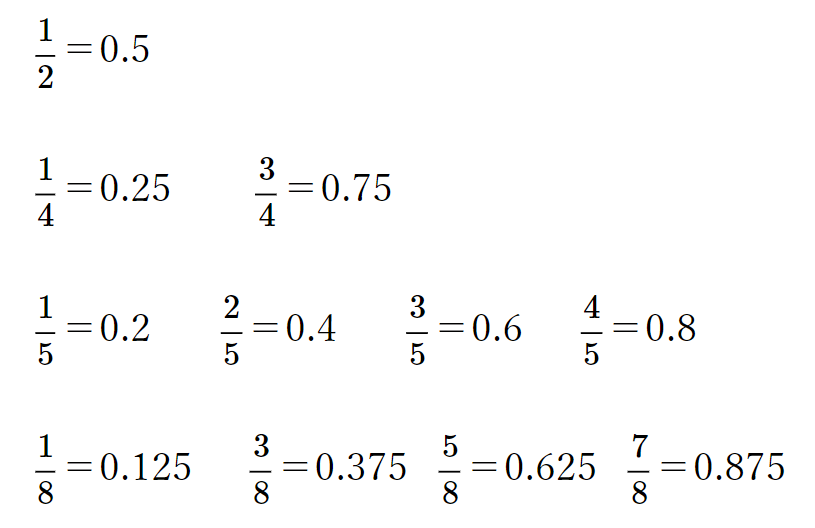
この部分は、毎回計算せずに、すぐに直せるようにしておきたい数字です。
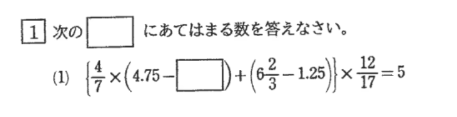
こちらは、2024年度三田国際第1回入試のはじめの問題です。
上記の計算問題のように、小数と分数が混ざった四則計算の出題は頻出です。
以下のような変換などは、すぐに分数に直して計算をしていくことになります。
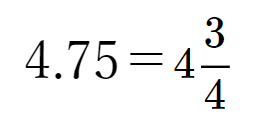
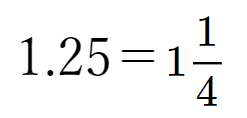
正確さ、スピードを考慮し、覚えるべきものは覚えておくことは中学受験算数において必要なことです。
問題解決能力の向上
「割合」を理解することは、実生活にもさまざまな場面で役立ちます。
「割合」の理解を深める第一歩として、日常生活の中でお子さんがイメージしやすいものと結びつけて考えることがとても大切です。たとえば、値引きの計算や成績の評価、人口統計など、私たちの生活に大きく関わっています。
野球が好きなお子さんなら、「打率」の考え方は身近でイメージしやすい例でしょう。
また、スーパーでの買い物の際、割引率を通じて「割合」が実生活に深く関わっていることを感じてもらえるかもしれません。
複数の概念との関連
割合は、比や平均、確率など他の数学的な概念とも関わりが深い分野です。
これらのつながりを考えられる力が求められるため、幅広い理解が必要です。
「割合」という大きなテーマの中には、入試で頻出の「食塩水の濃度」「売買算」「仕事算」「ニュートン算」などの単元も含まれています。
特にこれらの中で「比」の理解は、算数を得点源にするために欠かせない重要なポイントです。
比は中学受験において基礎的な概念でありながら、さまざまな問題に応用できる力であり、「図形」や「速さ」など多くの分野で活用されます。
比をしっかりと理解し、使いこなせるようになることで、受験対策も一層効果的になります。
また、比をしっかり学ぶことで算数に対する苦手意識が和らぎ、むしろ「算数が好き」になったり「得意」と感じるお子さんも多いです。
受験生にとって、比の重要性を理解し実践することが、受験成功の鍵となるでしょう。
入試問題の頻出テーマ
中学入試において「出題されない学校はない!」と言えるほど重要なテーマです。
特に、割合の問題は単なる文章題にとどまらず、図形問題などにも幅広く出題されます。
ここでは、2024年度の入試問題から一例をご紹介します。東京都港区にある人気のミッション系学校、東洋英和女学院の問題です。難問ではありませんが、割合の理解と条件を整理する力が求められる内容となっています。
<2024年 東洋英和女学院>
6年生が20点満点の試験を受けました。問1と問2は○が5点、×が0点、問3は○が10点、△が5点、×が0点です。次のことが分かっています。
- 問1が×の人は全体の12%で、全員が合計0点です。
- 問3が○の人は全体の8%で、全員20点満点です。
- 合計が5点の人は全体の16%で、合計0点の人より6人多い。
- 問3が×の人は、△の人の1.5倍より全体の2%多い。
- 平均点は9.6点です。
次の問いに答えなさい。
(1)試験を受けた人の人数を求めなさい。
(2)問3が△の人は何人ですか。
(3)合計15点の人は何人いますか。
また、神奈川県の男子トップ校のひとつ、聖光学院でも2024年度に「スーパーの売り上げデータ」を読み解く長文問題が出題されました。
さらに、公立の一貫校入試でもデータを読み解く力が問われる問題が増えています。
数学的なコミュニケーション
ちなみに、割合の問題を解くことで、数値を使ったコミュニケーション力も高まります。
友人や家族との情報交換やデータを正しく理解する上で、とても役立つ力です。
こうした理由から、割合の理解は中学受験でもとても大切になります。
しっかりした基礎を築くために、練習問題に取り組みながら理解を深めていくことをおすすめします。

